In this research axis we investigate energy transfer, conversion and storage at the quantum scale, and the interplay between energy and information. This is motivated by a continuous miniaturization of classical technologies, and the rise of quantum technologies, which demand a better understanding and control of energy (i.e. control heat flow, cooling, energy storage, catalysis, classical vs quantum resources).
In particular we address questions going from foundational issues such as foundation of quantum thermodynamics, resource theory, quantum limits to energy transfers, relation between information and thermodynamics, to more applied ones, such as the energetic cost of controlling quantum systems and implementation on setups such as optomechanical systems, superconducting systems and trapped ions.
Our overall goal is to achieve a multiscale complete understanding of energetics.
Coordinator: Dario Poletti
Energy conversion and storage
(Alexia AUFFEVES, Yvonne GAO, Mile GU, Manas MUKHERJEE, Nelly NG, Dario POLETTI, Maxime RICHARD)
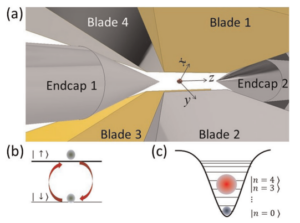
(a) Image of the ion trap set-up with a single ion acting as both an engine (the two-level system in panel b) and a load (the vibrational modes in panel c). Initially, when the ion is cooled near the ground state, the spread in occupation probabilities is small (smaller blue circle). After operating the energy-conversion device for a number of forward (engine type, as opposed to refrigerator type) cycles, the spread in occupation probabilities increases (larger, fuzzier, red circle).
As typically studied in classical thermodynamics, we investigate the conversion of heat into work in engines, refrigerators and heat pumps, but a scale in which quantum effects are significant and can potentially affect qualitatively the performance. We study the role of many-body properties of the working fluid, the use of measurements as baths, and how correlations affect the performance of the thermodynamic device.
Energy conversion is however not the only concern, as energy needs to be stored in carefully chosen degrees of freedom from which it can also be extracted. Furthermore, both the charging and discharging of a battery needs to occur as efficiently and effectively as possible.
Whether we study energy conversion or energy storage, we consider various experimental setups from superconducting qubits, trapped ions and optomechanical systems.
- N. Van Horne, D. Yum, T. Dutta, P. Hänggi, J. Gong, D. Poletti, M. Mukherjee, “Single-atom energy-conversion device with a quantum load”, npj Quantum Information 6, 37 (2020)
- J. Monsel, M. Fellous-Asiani, B. Huard, A. Auffèves, “The Energetic Cost of Work Extraction”, Phys. Rev. Lett. 124, 130601 (2020)
Foundations
(Alexia AUFFEVES, GONG Jiangbin, Mile GU, KWEK Leong Chuan, Hui Khoon NG, Nelly NG, Dario POLETTI, Marco TOMAMICHEL)
We ask ourselves fundamental questions about energetics and thermodynamics, including how the law of thermodynamics are affected by the presence between the different constituents of a system, e.g. system and baths, what are the bounds on the fluctuations in these non-equilibrium systems, and how measurements affect all of this.
Furthermore we also focus on the close tie between thermodynamics and information, starting from the principle that information is physical.
Importantly, fluctuation theorems impose constraints on possible work extraction probabilities in thermodynamical processes which are far stronger than the second law. Such constraints, can be bypassed if one allows for the use of additional degrees of freedom that may become correlated with the system from which work is extracted, but whose reduced state remains unchanged so that they can be re-used, i.e. catalysts.
- J.D. Jaramillo, J. Deng, J. Gong, “Quantum work fluctuations in connection with the Jarzynski equality”, Phys. Rev. E 96, 042119 (2017)
- P. Boes, R. Gallego, N.H.Y. Ng, J. Eisert, H. Wilming, “By-passing fluctuation theorems”, Quantum 4, 231 (2020)
- M. Tomamichel, “Quantum Relative Entropy: An Axiomatic Approach”, Lecture Notes (2022)
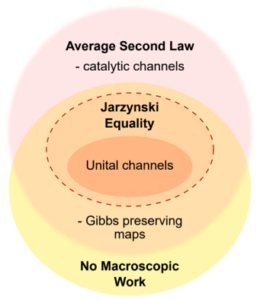
A summary of different regions of fluctuation relations depending on the allowed operations.
Energy transport
(GONG Jiangbin, Gabriel LEMARIE, Dario POLETTI)
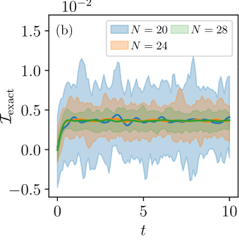

Current versus time for different realizations of two finite-size baths and for different sizes (top). The current converges to a single well-defined value as the baths size increases as shown by exponential decay of the current (bottom). From PRA 107, 022220 (2023)
We study transport properties in exotic materials including strongly correlated and/or topological quantum systems. Some of the issues we address are in what way and to what extent strong interactions or topological properties affect the transport properties of a system, and whether they can be used to control it, for example producing rectifiers.
We also address fundamental questions such as what are the conditions to observe the emergence of steady state currents and what are the key properties of a setup which affect them.
“Emergence of steady currents is a typical phenomenon which can be explained through the lens of pre-thermalization.”
- G. Landi, D. Poletti, G. Schaller, “Nonequilibrium boundary-driven quantum systems: Models, methods, and properties”, Rev. Mod. Phys. 94, 045006 (2022)
Cost of resources and control
(Alexia AUFFEVES, Yvonne GAO, Leong C. KWEK, Hui Khoon NG, Nelly NG, Dario POLETTI, Maxime RICHARD)
Understanding the resource required and consumed by a full stack of quantum computers is crucial to the development of quantum computers. Specifically, tackling both microscopic and macroscopic aspects requires both fundamental physics and engineering. In this axes we follow different approaches to achieve this task. One of these is the Metric-Noise-Resource (MNR) which is able to quantify and optimize all aspects of the full-stack quantum computer, bringing together concepts from quantum physics (e.g., noise on the qubits), quantum information (e.g., computing architecture and type of error correction), and enabling technologies (e.g., cryogenics, control electronics, and wiring).
“Quantum technologies must urgently plan for the creation and structuration of a transverse quantum energy initiative, connecting quantum thermodynamics, quantum information science, quantum physics, and engineering.”
An approach to study the effects of thermal baths on quantum systems is that of using bosonic linear thermal operations. This can allow to identify how thermal resources can also be used for non-thermal tasks as preparing quantum states.
- Y. Zheng, S. Campbell, G. De Chiara, D. Poletti, “Cost of counterdiabatic driving and work output”, Phys. Rev. A 94, 042132 (2016)
- M. Fellous-Asiani, J. H. Chai, Y. Thonnart, H. K. Ng, R. S. Whitney, A. Auffèves, “Optimizing resource efficiencies for scalable full-stack quantum computers « , arXiv:2209.05469 (2022)
- V. Narasimhachar, S. Assad, F. C. Binder, J. Thompson, B. Yadin and M. Gu, “Thermodynamic resources in continuous-variable quantum systems”, npj Quantum Information 7, 9 (2021)
- A. Auffèves, “Quantum Technologies Need a Quantum Energy Initiative”, PRX Quantum 3, 020101 (2022)
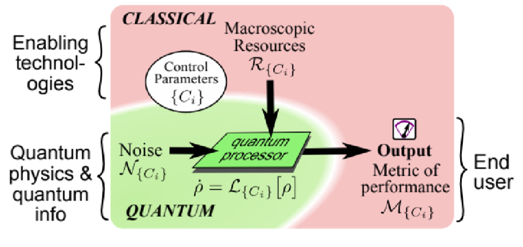
Metric-Noise-Resource methodology for the full-stack of a quantum computer

The transformation effected by the contents of the dashed box defines a generic bosonic linear thermal operation from an m-mode input system S to an m′–mode output system S′.
Keywords: Quantum fluids of light, polaritons, quantum optomechanics, trapped single atoms, ultracold gases, single-photon devices, superconducting qubits and architectures, integrated photonics, quantum sensors
